事故は企業価値を低下させる（ことがある）−その2【産業保安のけいざい学】 by 牧野 良次

さんぽコラム　産業保安のけいざい学
事故は企業価値を低下させる（ことがある）−その2
牧野良次

投稿日:2019年3月18日 17時30分

　 こんにちは。産総研の牧野です。随分時間がたってしまいましたが、前回コラム事故は企業価値を低下させる（ことがある）−その1の続きです。「事故は企業価値を下げるのではないか？」がコラムのテーマです。今回は、日本で起きた実際の事故を対象に、事故後の株価変動という観点から企業価値の低下を分析した研究（Makino, 2016）のさわりを紹介します。

前回コラムのおさらい

各企業の株価の動きはおおむね市場平均（日本で言えば日経平均株価）の動きと連動していると考えられています。もちろん各企業銘柄に特有の動きはあるものの、それは確率的な変動であると捉えます（これをマーケットモデルという）。

銘柄iの株価の、時刻t-1からtにかけての変化率をR_i,t、市場平均株価の変化率をR_m,t、銘柄iの株価変化率の時刻tにおける確率的変動をe_i,tとしてマーケットモデルを式で書けば以下のようになります。

R_i,t = α + βR_m,t + e_i,t

つまり、ある銘柄の株価変化率（R_i,t）は、市場平均と連動している部分（α + βR_m,t）とその銘柄の確率的変動の部分（e_i,t）に分けることができる、というモデル化です。次に行うべきことはデータを使って事故後のe_i,tを推定することです。事故後のe_i,tが大きくマイナスであれば、「事故」という銘柄特有のインパクトによって株価の伸び率がマイナスの影響を受けたと推論することができるでしょう。

分析の手順

• 事故発生日より十分以前の、各銘柄と市場平均の株価データを取得します（この研究では終値を使いました）。
• そのデータから各銘柄と市場平均の日間変化率（R_i,t, R_m,t）を計算します。
• さらにそのデータから回帰分析によってαとβの値を推定します。推定値をそれぞれα*、β*と名付けます（銘柄ごとにα*、β*は異なります）。
• α*とβ*、および事故日以降のR_m,tの実績値から、もし事故が起きていなければ実現していたであろうと推定されるR_i,tの理論値を算出します。これをR_i,t*と名付けます。R_i,t* = α* + β*R_m,tです。
• 事故日以降のR_i,t（実績値）とR_i,t*（理論値）の差を取って、事故によって引き起こされたと考えられる個別銘柄の変動e_i,t*を推定します。e_i,t* = R_i,t – R_i,t*です。
• 推定された各時点のe_i,t*について銘柄間の平均をとり、それをAAR_tと名付けます（AARはaverage abnormal returnの略）。
• AAR_tの事故後T日目までの累積値を計算します。それをCAAR_Tと名付けます（CAARはcumulative average abnormal returnの略）。
• CAAR_Tが統計的に有意にゼロから離れているか（特に、マイナスと言えるか）を検定します。

分析対象とした事故

上場している日本の化学会社において2005年から2012年の間に発生した爆発や火災を伴う事故がRISCADに43件収録されていました。そのうち25件は日本経済新聞に掲載されていなかったので除外し（株価の分析は広く報道されていることが前提です）、残りの18件の事故を分析対象としました。

事故は企業価値を低下させた（このサンプルでは）

事故が発生した日を起点として、事故から120日目までのCAARを示したのが下の図です。

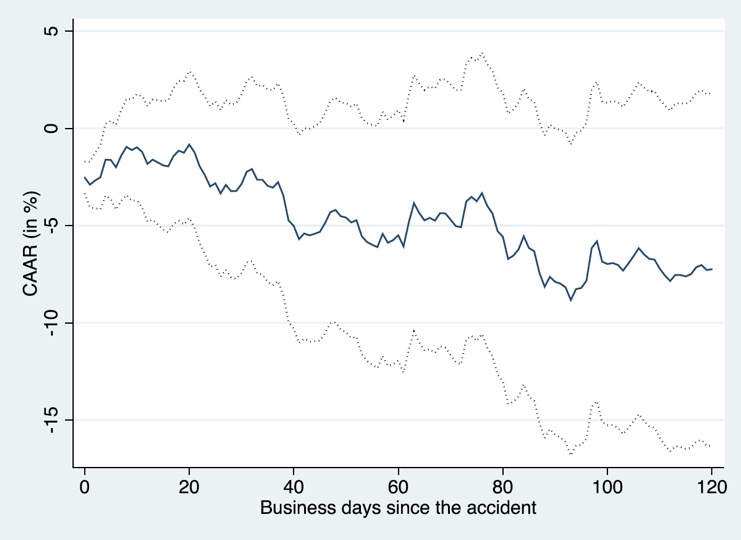
事故が発生した当日から3日後まで、CAARは統計的に有意にマイナスでした（有意水準1％）。18件の事故の平均として、事故のあと数日のあいだ、各銘柄の日間変化率は、もし事故が起きていなければそうなっていたであろうと推定される値よりも統計的に有意に低下していました。つまり、少なくともこのサンプルにおいては事故によって企業価値が有意に低下したという結果が得られました。

数値例による結果の解釈（その1）

例えば（あくまで数値例です）、もし事故が起きていなければ実現していたであろう、ある銘柄の日間変化率が1％だったとします（α* + β* R_m,tのこと）。しかし事故後の実際のデータでは−2％だったとしましょう（R_i,tの実績値のこと）。そうすれば事故によって引き起こされたと考えられる銘柄特有の変動は−3％と推定されます（e_i,t*のこと）。

数値例による結果の解釈（その2）

上のパーセンテージを適用してさらに数値例を示します。事故直前に株価時価総額100億円の企業があったとしましょう。もし事故が起きていなかったら時価総額はプラス1％で101億円になっていたと推定されます。しかし事故のあと実際は100億円のマイナス2％で98億円となりました。結局、101億円マイナス98億円の3億円分（100億円の3％）、事故による株価時価総額のマイナス＝企業価値の損失がでたということになります。

結果の解釈にあたっての注意点

時折、「事故があってもしばらく時間がたてば株価はもとに戻るでしょ？」という声を聞きます。どうせ戻るのであれば（極端に言えば）この種の分析をしても意味がない、というご意見なのかなと思います。しかしこれは解釈として十分ではありません。確かに、事故に起因すると考えられる銘柄特有の変動e_i,tは事故後しばらく時間が経過したら誤差の範囲に戻ると思われます。しかし、先ほどの数値例で言えば、事故がなければ101億円になっていたはずの株価時価総額が事故によって98億円に目減りしてしまっていることを忘れてはいけません。

事故のあと、市場平均（日本で言えば日経平均株価）の動きと連動している部分の株価変化率が1％のままであり、かつeit*が十分小さくなったとしましょう。このとき、もし事故が起きていなければ株価時価総額は101億円×1.01＝102.01億円になっていたと推定されます。それに対して事故が起きたあとは98億円×1.01 = 98.98億円に留まるわけです。98.98億円という数字を見て「98億円から回復しているじゃないか」という理解では十分ではなくて、「もし事故が起きていなければそもそも102.01億円になっていたはずだよね」ということまで考えるべきです。102.01億円−98.98億円＝3.03億円はあくまで損失として残っている（むしろ3億円から1％増えている）わけです。

参考文献
Makino, R., 2016. Stock market responses to chemical accidents in Japan: An event study. Journal of Loss Prevention in the Process Industries 44, 453-458.